Vector Fields

A way of representing functions with $2$- or $3$-dimensional inputs and outputs.

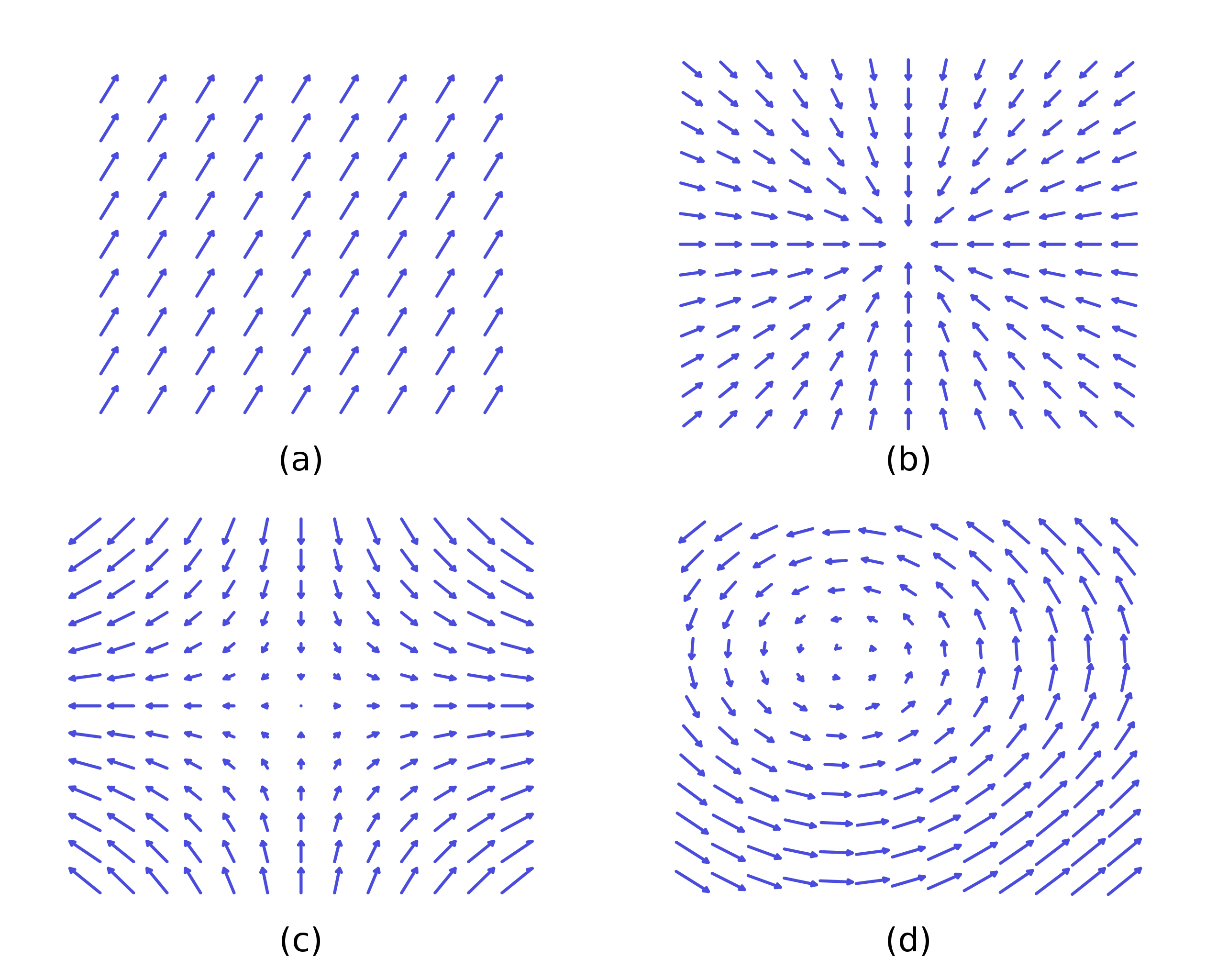
The coordinate system is the input space and the output is shown as vectors from a subset of the infinite points in the input space.

Conservative Fields

“When a scalar function can be converted into a vector field using a > gradient> ." - Cornelia’s Notes

Any line integral from point a to point be will always be the same.

$$\nabla f = \mathbf{F}$$ $f$: Potential function

See also this online resource.

Conditions for 3 Dimensions: $$ \begin{align} \frac{\partial f_{1}}{\partial y} = \frac{\partial f_{2}}{\partial x}, \ \frac{\partial f_{1}}{\partial z} = \frac{\partial f_{3}}{\partial x}, \ \frac{\partial f_{2}}{\partial z} = \frac{\partial f_{3}}{\partial y}, \end{align} $$

Conditions for 2 Dimensions: $$ \begin{align} \frac{\partial f_{1}}{\partial y} = \frac{\partial f_{2}}{\partial x} \end{align} $$

Notes

list
from #vectorfields
sort file.name