I integralregning finder man en funktions stamfunktion ($F(x)$). At integrere er det modsatte af at differentiere. Dvs. at $f(x)$ beskriver hældningen af $F(x)$. Integraler skrives således:
$$\int f(x) \ dx = F(x) + k$$
Det er vigtigt at huske $dx$ i integralet. Det er bare en skrivemåde, men det er forkert ikke at skrive det.
Noget andet der er vigtigt er at lægge $k$ til stamfunktionen. $k$ er bare en konstant, men den viser hvordan at man alligevel mister information når man integrere: hvis man kun har hældningen af en kurve, kan man godt generere den generalle form og hvor meget grafen stiger og falder, men man kan ikke finde startværdien for grafen.
Når man skriver svaret op med $k$ kalder man det den fuldstændige løsning.
At finde $k$
Hvis vi skal finde værdien af $k$ skal vi have et punkt. I dette eksempel er funktionen $f(x) = x^2$ og punktet $(2,10)$
Først integrerer vi $f(x)$
$$\int f(x) = \int x^2 = F(x) = \frac{x^3}{3}+k$$
Herefter kan vi sætte punktet ind i funktionen
$$F(2) = 10 \Longleftrightarrow \frac{2^3}{3}+k=10 \Longleftrightarrow 8+k=10 \Longleftrightarrow k = 2$$
Vi kan nu skrive $F(x)$ op med en specifik $k$-værdi. Dette kalder vi den partikulære løsning.
$$F(x)=\frac{x^3}{3}+2$$
Integration i Hånden
Mange simple funktioner kan integreres i hånden ved hjælp af et par regneregler. For eksempel kan $2x$ integreres således.
$$\int 2x \ dx= 2 \cdot \frac{x^2}{2} = x^2 + k$$
Bestemt Integrale
Et bestemt integrale kan udregne hvor meget $f(x)$ er vokset med i intervallet $a$ til $b$. Bestemte integraler kan skrives op sådan: $$\int_{a}^{b} f(x) \ dx = F(b) - F(a)$$
Arealet Under en Kurve
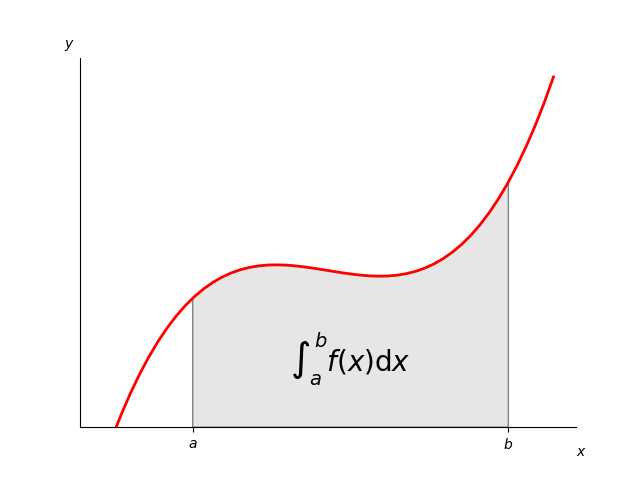
Man kan finde arealet under kurven $f(x)$, ved at tage det bestemte integrale af $f(x)$ hvor $a$ og $b$ afgrænser arealet som for illustrationen nedenfor.
Integraler og Bevægelse
Integraler kan bruges til at finde grafer for position fra en graf med acceleration på følgende måde.
Lad os sige at dette er vores funktion for acceleration $$a(t)$$
Vi kan nu finde $v(t)$ ved at integrere $a(t)$
$$\int a(t)\ dt = v(t) + k$$
For at finde funktionen for position ($s(t)$) kan vi igen integrere $v(t)$
$$\iint a(t)\ dt = \int v(t) + k\ dt = s(t) + kx + c$$